Diciembre 09, 2003
Tormento matemático
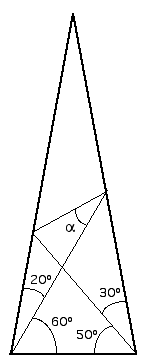 Escrito por Ricardo B. en Diciembre 9, 2003 07:02 PM
Escrito por Ricardo B. en Diciembre 9, 2003 07:02 PM
Con esos datos, llegamos a que alfa + beta = 110 y, usando el teorema de los senos, acabamos relacionando los senos de ambos ángulos. 2 ecuaciones, dos incógnitas. Todo tiene solución... hasta el aburrimiento :-)
Según tengo entendido a dicho problema no se le ha encontrado solución... Quizás fueras el primero ;)
Por cierto, dicho problema lo propuso Carlo Frabetti hace ya algunos años...
Hombre, no lo he terminado, la verdad. Pero si asignas una longitud de 1 al triángulo de abajo, el teorema de los senos te da las longitudes (relativas) de al menos dos líneas del triángulo que contiene a alfa, ¿no?
Al lado de abajo, quería decir. Si llegué a la relación de los ángulos, pero había mucho seno y la calculadora de windows es una mierda. Lo repasaré :-)
Cuando des con la solución ya me la apuntarás... Agradecido :) Te puedo decir que yo traté de averiguar el posible resultado midiendo con regla y transportador... Más que nada para tener una idea del valor final.. Pero de esto fue hace unos cuantos años, desde entonces no volví a intentarlo.
Referente a lo que todo tiene solución... pues no sé que decirte, hay bastantes retos matemáticos por resolver y algunos con recompensas económicas... sin ir más lejos, recientemente se resolvió el famoso teorema de Fermat, también el de los cuatro colores.
Si te animas podrías intentar trisecar un ángulo con regla y compás ;)